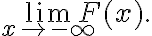BAC_TSM_ 2017

MEPU-A                                                 BACCALAURÉAT UNIQUE                          SESSION: 2017

SNECSO                   

PROFIL: SCIENCES MATHÉMATIQUES          ÉPREUVE DE : MATHS      DURÉE : 2 heures     Coefficient : 4

                                                                          Sujet

Exercice 1 : (4 points)

Soit  la fonction définie sur  par     

    1) Déterminer une primitive de  sur 

    2) Soit la suite  définie par    par :  . Exprimer  en fonction de

    3) Montrer que    est une suite décroissante positive . Que peut-on en déduire ? Calculer la limite de    lorsque 

        tend vers  .

    4) On pose : 

        a) Calculer   ,   et   . Exprimer    en fonction  de 

        b) Calculer la limite de    lorsque  tend vers  .

Exercice 2 : (4 points)

Une variable aléatoire  prend les valeurs 1 ; -1 et 2 avec les probabilités respectives

,  ,  , où  ,  ,   sont en progression arithmétique.

On suppose que l'espérance mathématique     de   est égal  à 1.

    1) Calculer   ,  ,     et la variance     de 

    2) Soient  ,  ,    trois points d'abscisse respectives 1 ; -1 et 2 d'une droite graduée  .

        a)  Calculer l'abscisse du point barycentre de  

        b) On pose ;   où  est un point de  . Montrer que

        c) Déterminer l'ensemble  des points  tels que 

Problème: (12 points)

Partie A

On considère la fonction  définie par  par  . On note  sa courbe représentative

dans le plan rapporté au repère orthogonal  .  L'unité graphique est 1 cm sur l'axe des abscisses et 10 cm sur l'axe des ordonnées.

    1)    a) On rappelle que   . Déterminer la limite de  en 

           b) Vérifier que pour tout réel  . Déterminer la limite de en

           c) En déduire que la courbe admet deux asymptotes que l'on précisera.

    2) On considère la fonction g définie sur l'intervalle    par  

          a) Démontrer que la fonction g est strictement décroissante sur l'intervalle  

          b) En déduire le signe lorsque  .

    3) Calculer   et l'exprimer en fonction de  ,   désignant la fonction dérivée de .

        En déduire le sens de variation de la fonction puis dresser son tableau de variation.

    4) Tracer les asymptotes à la courbe  et la courbe  .

Partie B

Soit la  la fonction définie sur par :  

    1) Étudier le sens de variation de la fonction 

    2) Vérifier que, pour tout nombre réel  ,     et calculer 

        a) En déduire , à l'aide d'une intégration par parties, le calcul de

        b) Vérifier que  peut s'écrire sous les formes suivantes :

    3) Déterminer   $\displaystyle \lim_{x \to -\infty} F(x).$.

    4) Déterminer 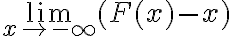 $\displaystyle \lim_{x \to -\infty} (F(x)-x)$. Donner une interprétation graphique de ce résultat.

         On donne :   .